
Trigonometri, üçgenlerin özelliklerini inceleyen bir matematik dalıdır. Trigonometri, geometri, fizik, mühendislik ve astronomi gibi birçok alanda uygulamaları olan önemli bir konudur. Bu haberde, trigonometri nedir, trigonometri formülleri nelerdir, trigonometri toplam fark formülleri, trigonometri değerleri, trigonometri cetveli, trigonometri tablosu ve trigonometri dönüşüm formülleri hakkında bilgi vereceğiz.
TRİGONOMETRİ NEDİR VE NASIL ORTAYA ÇIKTI?
Trigonometri, Yunanca “üçgen ölçümü” anlamına gelen bir kelimedir. Trigonometri, üçgenlerin kenarları ve açıları arasındaki ilişkileri bulmak için kullanılan bir matematik dalıdır. Trigonometri, antik çağlardan beri var olan bir konudur. Mısırlılar, Babililer, Hintliler, Çinliler ve Yunanlılar gibi eski uygarlıklar, astronomi, mimari, mühendislik ve denizcilik gibi alanlarda trigonometriyi kullanmışlardır. Trigonometri, modern matematikte de önemli bir rol oynamaktadır. Örneğin, karmaşık sayılar, Fourier serileri, dalga denklemleri ve diferansiyel denklemler gibi konular trigonometri ile ilgilidir.

TRİGONOMETRİ FORMÜLLERİ NELERDİR?
Trigonometri formülleri, üçgenlerin kenarları ve açıları arasındaki ilişkileri ifade eden eşitliklerdir. Trigonometri formülleri, üçgenlerin alanlarını, çevrelerini, yüksekliklerini, açıortaylarını, kenarortaylarını, açı kenar bağıntılarını, benzerlik kriterlerini, özel üçgenleri, çember içine ve dışına çizilen üçgenleri, üçgenlerin trigonometrik oranlarını, üçgenlerin genel çözümünü ve üçgenlerin analitik geometrisini bulmak için kullanılır. Trigonometri formülleri, aşağıdaki gibi sınıflandırılabilir:
Üçgenlerin Alan Formülleri
Üçgenlerin alan formülleri, üçgenlerin kenarları ve açıları ile alanlarını hesaplamak için kullanılan formüllerdir. Üçgenlerin alan formülleri, aşağıdaki gibidir:
Üçgenin alanı = (taban x yükseklik) / 2
Üçgenin alanı = (a x b x sinC) / 2
Üçgenin alanı = (b x c x sinA) / 2
Üçgenin alanı = (c x a x sinB) / 2
Üçgenin alanı = √(s x (s – a) x (s – b) x (s – c)), burada s = (a + b + c) / 2
Üçgenlerin Çevre Formülleri
Üçgenlerin çevre formülleri, üçgenlerin kenarlarının toplamını bulmak için kullanılan formüllerdir. Üçgenlerin çevre formülleri, aşağıdaki gibidir:
Üçgenin çevresi = a + b + c
Üçgenin çevresi = 2 x s, burada s = (a + b + c) / 2
Üçgenlerin Yükseklik Formülleri
Üçgenlerin yükseklik formülleri, üçgenlerin kenarları ve açıları ile yüksekliklerini hesaplamak için kullanılan formüllerdir. Üçgenlerin yükseklik formülleri, aşağıdaki gibidir:
Üçgenin yüksekliği = (2 x alan) / taban
Üçgenin yüksekliği = a x sinB
Üçgenin yüksekliği = b x sinA
Üçgenin yüksekliği = c x sinC
Üçgenlerin Açıortay Formülleri
Üçgenlerin açıortay formülleri, üçgenlerin kenarları ve açıları ile açıortaylarını hesaplamak için kullanılan formüllerdir. Üçgenlerin açıortay formülleri, aşağıdaki gibidir:
Üçgenin açıortayı = √((s x (s – a)) x (b x c)), burada s = (a + b + c) / 2
Üçgenin açıortayı = (2 x b x c x cosA) / (b + c)
Üçgenin açıortayı = (2 x c x a x cosB) / (c + a)
Üçgenin açıortayı = (2 x a x b x cosC) / (a + b)
Üçgenlerin Kenarortay Formülleri
Üçgenlerin kenarortay formülleri, üçgenlerin kenarları ve açıları ile kenarortaylarını hesaplamak için kullanılan formüllerdir. Üçgenlerin kenarortay formülleri, aşağıdaki gibidir:
Üçgenin kenarortayı = (a + b – c) / 2
Üçgenin kenarortayı = (b + c – a) / 2
Üçgenin kenarortayı = (c + a – b) / 2
Üçgenlerin Açı Kenar Bağıntıları
Üçgenlerin açı kenar bağıntıları, üçgenlerin kenarları ve açıları arasındaki orantılılığı ifade eden eşitliklerdir. Üçgenlerin açı kenar bağıntıları, aşağıdaki gibidir:
a / sinA = b / sinB = c / sinC
a / b = sinA / sinB
b / c = sinB / sinC
c / a = sinC / sinA
Üçgenlerin Benzerlik Kriterleri
Üçgenlerin benzerlik kriterleri, iki üçgenin benzer olup olmadığını belirlemek için kullanılan kurallardır. İki üçgenin benzer olması için, karşılık gelen açılarının eşit ve karşılık gelen kenarlarının orantılı olması gerekir. Üçgenlerin benzerlik kriterleri, aşağıdaki gibidir:
-Açı-Açı (AA) Kriteri: İki üçgenin iki açısı da eşitse, üçgenler benzerdir.
-Kenar-Kenar (KK) Kriteri: İki üçgenin iki kenarı da orantılı ve aralarındaki açılar eşitse, üçgenler benzerdir.
-Kenar-Açı-Kenar (KAK) Kriteri: İki üçgenin bir kenarı orantılı ve aralarındaki açılar eşitse, üçgenler benzerdir.
-Kenar-Kenar-Kenar (KKK) Kriteri: İki üçgenin üç kenarı da orantılıysa, üçgenler benzerdir.
Özel Üçgenler
Özel üçgenler, bazı özellikleri nedeniyle diğer üçgenlerden ayrılan üçgenlerdir. Özel üçgenler, aşağıdaki gibi sınıflandırılabilir:
-Dik Üçgen: Bir açısı 90 derece olan üçgendir. Dik üçgenlerde, Pisagor teoremi geçerlidir. Pisagor teoremi, dik üçgenin hipotenüsünün karesinin, dik kenarların karelerinin toplamına eşit olduğunu söyler. Pisagor teoremi, aşağıdaki gibi ifade edilir: a^2 + b^2 = c^2, burada a ve b dik kenarlar, c hipotenüstür.
-Eşkenar Üçgen: Üç kenarı da eşit olan üçgendir. Eşkenar üçgenlerde, üç açı da 60 derecedir. Eşkenar üçgenlerin alanı ve yüksekliği, aşağıdaki gibi bulunur:
-Üçgenin alanı = (√3 x a^2) / 4, burada a kenardır.
-Üçgenin yüksekliği = (√3 x a) / 2, burada a kenardır.
-İkizkenar Üçgen: İki kenarı eşit olan üçgendir. İkizkenar üçgenlerde, eşit kenarların karşısındaki açılar da eşittir. İkizkenar üçgenlerin alanı ve yüksekliği, aşağıdaki gibi bulunur:
-Üçgenin alanı = (b x h) / 2, burada b taban, h yüksekliktir.
-Üçgenin yüksekliği = √(a^2 – (b^2 / 4)), burada a eşit kenar, b tabandır.
-30-60-90 Üçgen: Bir açısı 30 derece, bir açısı 60 derece ve bir açısı 90 derece olan üçgendir. 30-60-90 üçgenlerde, kenarlar arasında aşağıdaki orantı vardır: x : x√3 : 2x, burada x en kısa kenar, x√3 orta kenar, 2x hipotenüstür.
-45-45-90 Üçgen: İki açısı 45 derece ve bir açısı 90 derece olan üçgendir. 45-45-90 üçgenlerde, kenarlar arasında aşağıdaki orantı vardır: x : x : x√2, burada x dik kenarlar, x√2 hipotenüstür.

ÇEMBER İÇİNE VE DIŞINA ÇİZİLEN ÜÇGENLER
Çember içine çizilen üçgen, çemberin çevresine değen üçgendir. Çember içine çizilen üçgenlerde, aşağıdaki özellikler geçerlidir:
-Çemberin merkezi, üçgenin kenarortaylarının kesişme noktasıdır.
-Çemberin yarıçapı, üçgenin açıortaylarının uzunluğuna eşittir.
-Çemberin çevresi, üçgenin çevresinin yarısına eşittir.
-Çemberin alanı, üçgenin alanının iki katına eşittir.
Çember dışına çizilen üçgen, çemberin merkezini içeren üçgendir. Çember dışına çizilen üçgenlerde, aşağıdaki özellikler geçerlidir:
-Çemberin merkezi, üçgenin yüksekliklerinin kesişme noktasıdır.
-Çemberin yarıçapı, üçgenin hipotenüsünün yarısına eşittir.
-Çemberin çevresi, üçgenin çevresine eşittir.
-Çemberin alanı, üçgenin alanının dört katına eşittir.
ÜÇGENLERİN TRİGONOMETRİK ORANLARI
Üçgenlerin trigonometrik oranları, üçgenlerin açıları ile kenarları arasındaki oranları ifade eden fonksiyonlardır. Üçgenlerin trigonometrik oranları, aşağıdaki gibidir:
-Sinüs: Bir açının karşısındaki dik kenarın, hipotenüse oranıdır. Sinüs, aşağıdaki gibi ifade edilir: sinA = a / c, burada a karşı kenar, c hipotenüstür.
-Kosinüs: Bir açının yanındaki dik kenarın, hipotenüse oranıdır. Kosinüs, aşağıdaki gibi ifade edilir: cosA = b / c, burada b yan kenar, c hipotenüstür.
-Tanjant: Bir açının karşısındaki dik kenarın, yanındaki dik kenara oranıdır. Tanjant, aşağıdaki gibi ifade edilir: tanA = a / b, burada a karşı kenar, b yan kenardır.
-Kotanjant: Bir açının yanındaki dik kenarın, karşısındaki dik kenara oranıdır. Kotanjant, aşağıdaki gibi ifade edilir: cotA = b / a, burada b yan kenar, a karşı kenardır.
-Sekant: Bir açının hipotenüsünün, yanındaki dik kenara oranıdır. Sekant, aşağıdaki gibi ifade edilir: secA = c / b, burada c hipotenüs, b yan kenardır.
-Kosekant: Bir açının hipotenüsünün, karşısındaki dik kenara oranıdır. Kosekant, aşağıdaki gibi ifade edilir: cscA = c / a, burada c hipotenüs, a karşı kenardır.
ÜÇGENLERİN GENEL ÇÖZÜMÜ
Üçgenlerin genel çözümü, üçgenlerin kenarları ve açıları arasındaki ilişkileri kullanarak, üçgenin tüm bilinmeyenlerini bulmak için kullanılan yöntemdir. Üçgenlerin genel çözümü, aşağıdaki adımları izler:
-Üçgenin verilen bilgilerini tanımla. Örneğin, üçgenin bir kenarı ve iki açısı verilmişse, bu AAS (Açı-Açı-Kenar) durumudur.
-Üçgenin kalan bilgilerini bulmak için uygun trigonometri formüllerini kullan. Örneğin, AAS durumunda, kalan kenarları ve açıyı sinüs kuralı ile bulabilirsin.
-Üçgenin çözümünü kontrol etmek için, üçgenin kenarlarının ve açılarının toplamlarını hesapla. Örneğin, üçgenin kenarlarının toplamı çevresine, üçgenin açılarının toplamı 180 dereceye eşit olmalıdır.
ÜÇGENLERİN ANALİTİK GEOMETRİSİ
Üçgenlerin analitik geometrisi, üçgenlerin koordinat düzlemindeki konumlarını ve özelliklerini inceleyen bir konudur. Üçgenlerin analitik geometrisi, aşağıdaki gibi sınıflandırılabilir:
Üçgenin Koordinatlarının Bulunması
Üçgenin koordinatlarının bulunması, üçgenin kenarlarının veya açılarının denklemlerini kullanarak, üçgenin köşe noktalarının koordinatlarını bulmak için kullanılan yöntemdir. Üçgenin koordinatlarının bulunması, aşağıdaki adımları izler:
Üçgenin kenarlarının veya açılarının denklemlerini yaz. Örneğin, üçgenin bir kenarı y = 2x + 3, diğer kenarı y = -x + 5 ve üçüncü kenarı x = 4 ise, bu denklemleri kullanabilirsin.
Üçgenin köşe noktalarının koordinatlarını bulmak için, kenarların denklemlerini eşitle. Örneğin, y = 2x + 3 ve y = -x + 5 denklemlerini eşitleyerek, bir köşe noktasının koordinatlarını (1, 5) olarak bulabilirsin.
Üçgenin alanını, çevresini, açılarını ve diğer özelliklerini bulmak için, üçgenin koordinatlarını kullan. Örneğin, üçgenin alanını bulmak için, determinant formülünü kullanabilirsin:
Üçgenin alanı = |(x1 x y1 1) (x2 y2 1) (x3 y3 1)| / 2, burada (x1, y1), (x2, y2) ve (x3, y3) üçgenin köşe noktalarıdır.
Üçgenin Denklemlerinin Bulunması
Üçgenin denklemlerinin bulunması, üçgenin köşe noktalarının koordinatlarını kullanarak, üçgenin kenarlarının veya açılarının denklemlerini bulmak için kullanılan yöntemdir. Üçgenin denklemlerinin bulunması, aşağıdaki adımları izler:
Üçgenin köşe noktalarının koordinatlarını tanımla. Örneğin, üçgenin köşe noktaları (1, 5), (4, 3) ve (4, 7) ise, bu koordinatları kullanabilirsin.
Üçgenin kenarlarının veya açılarının denklemlerini bulmak için, doğru denklemi veya açıortay denklemi gibi uygun formülleri kullan. Örneğin, üçgenin bir kenarının denklemini bulmak için, iki noktadan geçen doğru denklemini kullanabilirsin:
y – y1 = m (x – x1), burada m eğim, (x1, y1) doğrunun geçtiği bir noktadır.
SIKÇA SORULAN SORULAR
Trigonometri nedir?
Trigonometri, üçgenlerin özelliklerini inceleyen bir matematik dalıdır.
Trigonometri formülleri nelerdir?
Trigonometri formülleri, üçgenlerin kenarları ve açıları arasındaki ilişkileri ifade eden eşitliklerdir.
Trigonometri toplam fark formülleri nelerdir?
Trigonometri toplam fark formülleri, iki açının toplamı veya farkı ile ilgili trigonometrik fonksiyonları basitleştirmek için kullanılan formüllerdir. Örneğin, sin(A + B) = sinA cosB + cosA sinB formülü bir toplam fark formülüdür.
Trigonometri değerleri nelerdir?
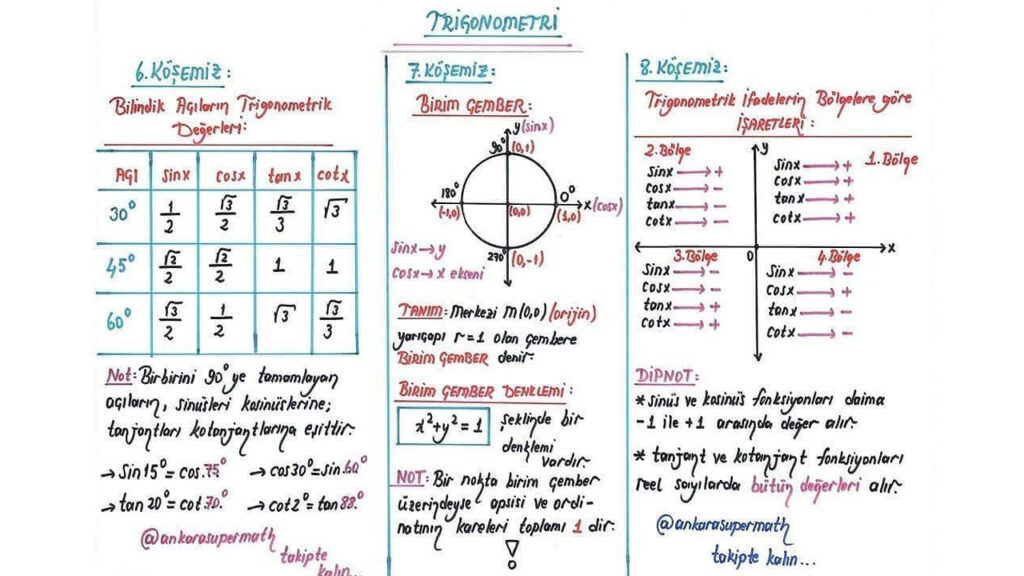
Trigonometri değerleri, belirli açılar için trigonometrik fonksiyonların aldığı değerlerdir. Örneğin, 30 derece için sin30 = 1/2, cos30 = √3/2, tan30 = 1/√3 değerleridir.
Trigonometri cetveli nedir?
Trigonometri cetveli, belirli açılar için trigonometrik fonksiyonların değerlerini gösteren bir tablodur. Örneğin, aşağıdaki tablo bir trigonometri cetvelidir…
Trigonometri tablosu nedir?
Trigonometri tablosu, trigonometrik fonksiyonların değerlerini farklı açılar ve kenarlar için gösteren bir tablodur. Örneğin, aşağıdaki tablo bir trigonometri tablosudur…
| Açı | Sinüs | Kosinüs | Tanjant | Kotanjant | Sekant | Kosekant |
| 0 | 0 | 1 | 0 | Tanımsız | 1 | Tanımsız |
| 30 | 1/2 | √3/2 | 1/√3 | √3 | 2/√3 | 2 |
| 45 | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60 | √3/2 | 1/2 | √3 | 1/√3 | 2 | 2/√3 |
| 90 | 1 | 0 | Tanımsız | 0 | Tanımsız | 1 |
Trigonometri dönüşüm formülleri nelerdir?
Trigonometri dönüşüm formülleri, trigonometrik fonksiyonları birbirine dönüştürmek için kullanılan formüllerdir. Örneğin, tanA = sinA / cosA formülü bir dönüşüm formülüdür.
Trigonometri esas ölçü nedir?
Trigonometri esas ölçü, trigonometrik fonksiyonların değerlerinin değişmediği, 0 ile 360 derece arasındaki en küçük pozitif açıdır. Örneğin, 390 derecenin esas ölçüsü 30 derecedir.
TRİGONOMETRİ HAKKINDA
Trigonometri, matematikte ve diğer bilim dallarında çok önemli bir konudur. Trigonometri, üçgenlerin özelliklerini ve uygulamalarını anlamamızı sağlar. Trigonometri, birçok formül, tablo, cetvel ve yöntem içerir. Bu haberde, trigonometri nedir, trigonometri formülleri nelerdir, trigonometri toplam fark formülleri, trigonometri değerleri, trigonometri cetveli, trigonometri tablosu ve trigonometri dönüşüm formülleri hakkında bilgi verdik. Ayrıca, üçgenlerin genel çözümü, analitik geometrisi, özel üçgenleri ve çember içine ve dışına çizilen üçgenleri de anlattık. Trigonometri ile ilgili daha fazla bilgi için, aşağıdaki kaynaklara bakabilirsiniz:


